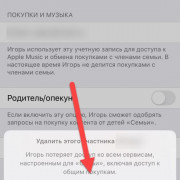
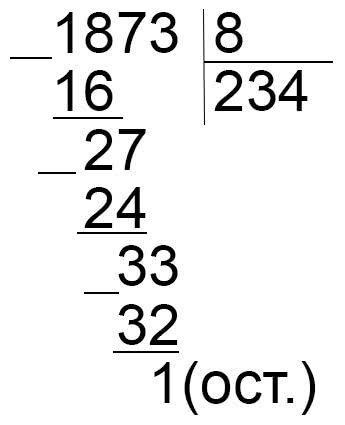Деление на двузначное число

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

1. Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
2. Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
3. 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
4. Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
5. К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
6. Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
7. 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Деление на двузначное число — сложная операция, требующая тренированной памяти для запоминания начальной и промежуточной
информации.

Как и в других разделах, начинайте с отработки наиболее простых упражнений, параллельно осваивая более сложные.

Методика деления

При устном делении запоминайте цифры парами разрядов, например, 3542 как «тридцать пять — сорок два».

Если делимое четырехзначное, то первым делом определите число сотен в ответе, поделив первую пару цифр на делитель. Дальше работайте с остатком от этого деления и второй парой. Например, при делении 3542 на 11, число сотен в ответе — 3, а деление 242 на 11 дает 22, то есть ответ — 322.

Способы деления для различных комбинаций чисел даны в следующих примерах.

На первом этапе не обращайте внимания на остатки от деления — на практике обычно достаточно приближенного ответа.

Во всех примерах в круглых скобках
показывается остаток от деления.

Деление на 11-19

A.1.
Умножение до 19×9.

Деление — операция, обратная умножению. Выучите наизусть таблицу умножения до 19×9 — это позволит быстро делить на числа, меньшие 20. Для тренировки используйте пример:

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.

Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?

Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.

Решите задачу самостоятельно.

Проверь себя.

S пола = 7 ∙ 8 = 56 (м²)

S лам. = 50 ∙50 = 2 500 (см²)

1 м² = 10 000 см²

10 000 : 2 500 = 4 (шт.) – ламината в 1 м².

56 ∙ 4 = 224 (шт.) – ламината потребуется.

Ответ: 224 штук ламината.

Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.

Выразим 3 кг в граммах.

1 кг = 1 000 г

3 кг = 3 000 г

35 ∙ 100 = 3 500 (г) – краски потребуется.

3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.

Ответ: 500 г краски не хватит.

Решите аналогичную задачу самостоятельно и проверьте по образцу.

Задача

Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.

3 + 4 = 7 (м²) – занимают окно и дверь.

80 – 7 = 73 (м²) – нужно оклеить обоями.

7 ∙ 10 = 70 (м²) – в семи рулонах.

73 – 70  = 3 (м²) – обоев не хватит.

Ответ: не хватит 3 м².

Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!

(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =

640 ∙5 ∙0 +640 : 1 – 630 =

? + 150 – 240 – 10 + 26 = 526

Проверь себя.

0, 10, 600.

Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!

В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).

В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082: 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как делить столбиком меньшее число на большее?

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

Как делить столбиком числа с нулями?

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

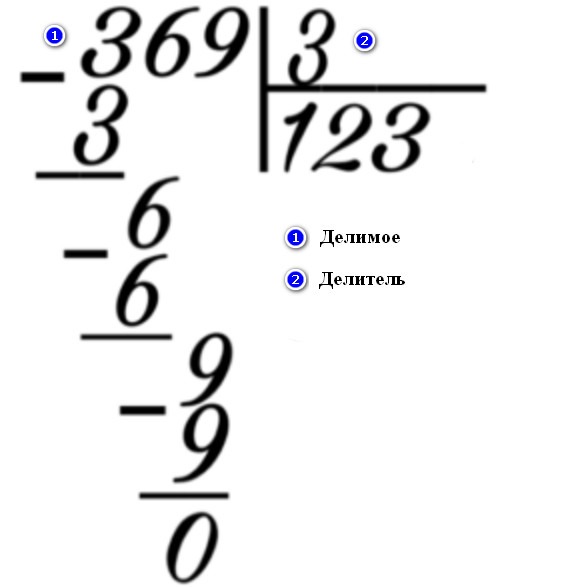
Еще один пример деления

Правило встречается в следующих упражнениях:

2 класс

Страница 67. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. Вариант 2. № 1,
Моро, Волкова, Проверочные работы

Страница 29. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 40. Вариант 1. № 6,
Моро, Волкова, Проверочные работы

Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 13. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 85. Вариант 2. Тест 3,
Моро, Волкова, Проверочные работы

Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 36,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1,
Мерзляк, Полонский, Якир, Учебник

Упражнение 520,
Мерзляк, Полонский, Якир, Учебник

Упражнение 656,
Мерзляк, Полонский, Якир, Учебник

Упражнение 657,
Мерзляк, Полонский, Якир, Учебник

Упражнение 673,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1050,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Решим пример \(\textcolor{red} {295383\div 34}\).

Далее записываем известные
компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor{red} {8\cdot 37=272}\). Записываем его под 295 и находим разницу: \(\textcolor{red} {295-272=23}\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия \(\textcolor{red} {295383\div 34=8687}\) и 25 в остатке.

Рассмотрим еще один пример. \(\textcolor{red} {25326\div 63}\).

Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.

Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать , поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.

Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.

126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления \(\textcolor{red} {25326\div 63=402}\).

Итак, в общем виде алгоритм деления в столбик выглядит так:1. Находим первое неполное делимое и количество цифр в частном.2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.4. Ставим между ними знак минус и выполняем действие.5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.7. Если неполное делимое невозможно разделить на делитель, то в частном ставится и к этому неполному делимому сносится следующая цифра.

Примеры на деление четырехзначного числа на двузначное с остатком с ответами:

Те же самые примеры на деление одного числа на другое с остатком, что приведены выше, но с ответами для быстрой проверки решений.

2400 : 85 = 28 остаток 203882 : 22 = 176 остаток 103345 : 39 = 85 остаток 307032 : 26 = 270 остаток 122725 : 80 = 34 остаток 55826 : 56 = 104 остаток 27292 : 11 = 662 остаток 108586 : 49 = 175 остаток 115797 : 85 = 68 остаток 175751 : 47 = 122 остаток 173445 : 84 = 41 остаток 15596 : 65 = 86 остаток 61743 : 13 = 134 остаток 12455 : 70 = 35 остаток 52227 : 78 = 28 остаток 431512 : 13 = 116 остаток 45677 : 23 = 246 остаток 191486 : 69 = 21 остаток 373141 : 87 = 36 остаток 94132 : 98 = 42 остаток 167653 : 65 = 117 остаток 488141 : 73 = 111 остаток 389029 : 64 = 141 остаток 57816 : 19 = 411 остаток 72164 : 50 = 43 остаток 14

2767 : 84 = 32 остаток 799120 : 37 = 246 остаток 184368 : 23 = 189 остаток 213993 : 17 = 234 остаток 154873 : 89 = 54 остаток 679870 : 76 = 129 остаток 668507 : 14 = 607 остаток 97281 : 70 = 104 остаток 15790 : 25 = 231 остаток 153567 : 13 = 274 остаток 53295 : 81 = 40 остаток 553691 : 62 = 59 остаток 336601 : 35 = 188 остаток 212155 : 25 = 86 остаток 55754 : 96 = 59 остаток 908932 : 12 = 744 остаток 49323 : 78 = 119 остаток 412035 : 89 = 22 остаток 779347 : 94 = 99 остаток 419640 : 32 = 301 остаток 87326 : 59 = 124 остаток 108386 : 43 = 195 остаток 18628 : 68 = 126 остаток 606711 : 21 = 319 остаток 125529 : 84 = 65 остаток 69

Сгенерировано примеров на деление четырехзначного числа на двузначное с остатком с ответами в качестве тренажера по математике: 50

Скачать

Распечатать

На этой странице сайта результат работы генератора случайных примеров по математике на деление четырехзначного числа на двузначное с остатком для тренировки арифметических действий учениками 1, 2, 3, 4 классов средней общеобразовательной школы.

Тренировочные примеры по математике на деление четырехзначного числа на двузначное с остатком для учеников первого, второго, третьего, четвертого класса можно отображать для распечатки или скачивания в два, три или четыре столбца.

Математические примеры на деление четырехзначного числа на двузначное с остатком, которые приведены на этой странице сайте, могут использоваться в качестве тренажера для отработки арифметических действий учителями, преподавателями, родителями или репетиторами для учащихся 1-го, 2-го, 3-го, 4-го класса.

Задания на деление четырехзначного числа на двузначное с остатком, которые находятся в этом разделе сайта, можно использовать в карточках на уроках математики для закрепления пройденного материала.

Как пошагово объяснить алгоритм математического действия?

Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:

Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части

Важно указать ребенку, что ответ не должен превышать 9.
Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
Далее, нужно найти разницу между частью делимого и полученным произведением.
Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.