Умножение в столбик

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
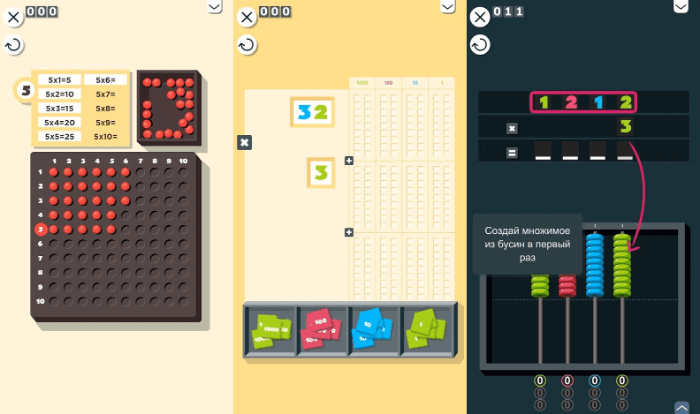
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1

Выполняем умножение столбиком, не обращая внимание на запятые

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63,37 и ,12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3,37·,12=7,6044.

Пример 5

Подсчитайте, сколько будет 3,2601 умножить на ,0254.

Решение 

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3,2601·,0254=,08280654.

Умножение суммы на число

Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?

Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:

Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.

Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.

Таким способом удобно умножать большие величины.

Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.

Умножайте сначала десятки, потом единицы, произведения складывайте.

Как это сделать, рассмотрите на примере.

Сумму десяти и пяти умножим на шесть.

Это распределительное свойство умножения суммы на число.

Правило умножения суммы на число запишите буквенным выражением.

За внимание награждаю вас оранжевой лентой

Идите по маршруту дальше.

Деление суммы на число

Прочитайте рассказ «Из истории символов».

Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление»

Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие. 

В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».

Для записи действия применяются разные знаки:

В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.

Познакомимся со способом деления. Выполните задание.

Какие числа нужно вставить в «окошки», чтобы получились верные равенства?

Решение.

Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.

Подсказка: вспомните результаты табличного умножения на 3. Например, 27.

Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.

Запишите подробное решение:

Сформулируйте правило деления суммы на число:

Голубой цвет неба на маршруте вам не помешает.

Карточки по математике Деление столбиком

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Выполнить деление столбиком

486 : 2 642 :2 693 : 3

848 : 4 936 : 3 264 : 2

530 : 5 856 : 8 648 : 6

836 : 4 972 : 9 675 : 5

Номер материала: ДБ-1199013

Не нашли то что искали?

Вам будут интересны эти курсы:

Вы здесь

Умножение в столбик

Сегодня существуют специальные сервисы, на которых достаточно просто ввести значения в пустые поля, а решение примера в столбик будет составлено автоматически и появится на той же странице, некоторые сайты позволяют получить полностью расписанный процесс умножения в столбик, например можно

Ниже будет описано, как же на сегодняшний день принято выполнять умножение в столбик и записывать это.

Умножения столбиком позволяет упростить умножения чисел. Метод подразумевает последовательное умножение первого числа, на все цифры второго числа, после которого суммируют полученные значения произведений с учетом «отступа». Рассмотрим на том же примере, как это осуществляется.
Для начала умножаем 6 на 9, получаем 54. 4 записываем, 5 запоминаем. Затем умножаем 7 на 9, получаем 63. Но у нас еще есть отложенное число 5. Прибавляем его к 63, получаем 68. Таким образом, перед четверкой записываем 68. Получаем опять тот же результат 684. Теперь приведем пример посложнее. Умножим 76 на 95. Умножение производится поэтапно: Сначала умножаем 76 на 5. Результат 380. Записываем его в строку.
Теперь 9 умножим на 7, получим 684. Записываем во вторую строку со сдвигом, так как производили умножение десятков.
Последним действием будет их сложение. Итого 7220.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Как делить в столбик с остатком?

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Деление с остатком

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

слайд из презентации о делении чисел с остатком

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Решим пример \(\textcolor{red} {295383\div 34}\).

Далее записываем известные
компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor{red} {8\cdot 37=272}\). Записываем его под 295 и находим разницу: \(\textcolor{red} {295-272=23}\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия \(\textcolor{red} {295383\div 34=8687}\) и 25 в остатке.

Рассмотрим еще один пример. \(\textcolor{red} {25326\div 63}\).

Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.

Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать , поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.

Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.

126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления \(\textcolor{red} {25326\div 63=402}\).

Итак, в общем виде алгоритм деления в столбик выглядит так:1. Находим первое неполное делимое и количество цифр в частном.2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.4. Ставим между ними знак минус и выполняем действие.5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.7. Если неполное делимое невозможно разделить на делитель, то в частном ставится и к этому неполному делимому сносится следующая цифра.

Как умножать столбиком?

Чтобы умножать столбиком, достаточно знать таблицу умножения от 1 до 10 и несложное правило: многозначные числа можно перемножать по разрядам. Повогорим более подробно о правилах умножения в столбик. 

Пример 1

16 х 21.

Сначала 16 умножаем на 1, получаем 16. Потом 16 умножаем на 20, получаем 320. Складываем два этих результата:

16 + 320 = 336.

Это и есть умножение по разрядам: первый множитель умножается по очереди на все цифры второго множителя, начиная с младшего разряда, а потом полученные результаты складываются.

Если записать пример 1 в столбик, получим следующее:

Здесь самое главное – аккуратная запись. Разряды единиц должны писаться под единицами, десятки – под десятками и т.д. Потом идёт сложение по разрядам:

0 при умножении на 20 писать не обязательно, можно умножить просто на 2, но результаты сдвинуть влево на 1 разряд.

Пример 2

Более сложный пример: 24 х 328. Большее число лучше сделать множимым, а меньшее – множителем: так нужно будет складывать только 2 числа, а не 3. Хотя можно и наоборот, т.к. от перемены мест слагаемых или множителей результаты не меняются. Итак:

Здесь умножение получилось более трудным. 8 х 4 = 32. Мы записали только 2, а 3 держим в уме: эту тройку нужно будет прибавить к результату перемножения десятков.

Затем умножили 4 х 2 = 8, да 3 у нас в уме. Складываем десятки, получаем: 8 + 3 = 11. И опять в разряд десятков пишем только 1, а вторую единицу, которая у нас пойдёт в разряд сотен, держим в уме, не забываем.

Теперь нужно точно так же 328 умножить на 20 или на 2 со сдвигом записи на 1 разряд влево. И сложить результаты.

Развитие памяти тренажёр и теория

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 3/5 на 0,9.

Как решаем:

1. Записать 0,9 в виде обыкновенной дроби:

   0,9 = 9/10.

2. Умножить числа по правилам
   3/5 ∗ 9/10 = 27/50 = 0,54.

Ответ: 3/5 ∗ 0,9 = 0,54.

Пример 2. Умножить 0,18 на 3 1/4.

Как решаем:

1. Записать 3 1/4 в виде десятичной дроби:

   3 1/4 = 3,25.

2. Произвести умножение в столбик или при помощи калькулятора:

   0,18 ∗ 3,25 = 0,585.

Ответ: 0,18 ∗ 3 1/4 = 0,585.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Проверочные работы по математике на тему “Умножение и деление многозначных чисел”(4 класс)

Самостоятельная работа по теме: «Умножение и деление на двузначное число»

4 класс, 3 четверть

вариант I

1. Решите пример на деление:

336 : 3 = 138 : 46 =

750 : 50 = 640 : 80 =

1. Решите пример на умножение:

132 * 59 = 631 * 60 =

72 * 20 = 86 * 26 =

1. Решите задачу:

На склад поступило 2 тонны 640 кг муки. Затем 13 мешков по 48 кг в каждом отдали в производство. Сколько муки осталось на складе?

1. Решите задачу:

Из точки А и точки В на встречу друг другу одновременно выехали 2 велосипедиста. Расстояние между точками равно 200 км. Они встретились через 5 часов. С какой скоростью двигался первый велосипедист, если скорость второго была равна 18 км/час?

1. Найдите значение выражений:

32 568 – (2 832 * 7 + 3 202 : 2) = (1652 * 7 – 237 : 3) – 238 =

вариант II

1. Решите пример на деление:

350 : 50 = 230 : 46 =

483 : 3 = 320 : 80 =

2. Решите пример на умножение:

47 * 30 = 312 * 61 =

245 * 30 = 48 * 27 =

3. Решите задачу:

На склад в магазин привезли 2830 кг сахара. Каждый день продавали по 68 кг. Сколько сахара осталось на складе после 23 дней?

4. Решите задачу:

Из двух населенных пунктов на встречу друг другу вышли 2 путника. Расстояние между населенными пунктами равно 84 км. Они встретились через 6 часов. С какой скоростью шел первый путник, если скорость второго была равна 8 км/час?

5. Найдите значение выражений:

18 345 – (5 358 * 2 + 3 208 : 2 ) = (6 785 * 3 – 8 120 : 4) – 2 458 =

вариант III

1. Решите пример на деление:

276 : 46 = 840 : 40 =

453 : 3 = 990 : 30 =

2. Решите пример на умножение:

186 * 35 = 23 * 80 =

43 * 50 = 134 * 70 =

3. Решите задачу:

В цех привезли 3 654 заготовки. В токарный цех каждый день направляют по 37 деталей. Сколько деталей осталось в цеху через 40 дней?

4. Решите задачу:

Из двух городов на встречу друг другу выехали 2 мотоциклиста. Расстояние между городами равно 840 км. Они встретились через 7 часов. С какой скоростью ехал первый мотоциклист, если скорость второго была равна 70 км/час?

5. Найдите значение выражений:

29 235 – (3 984 * 6 + 6 788 : 2 ) = (8 102 – 246 : 3) – 315 * 4 =

Самостоятельная работа по теме: «Умножение и деление на трёхзначное число»

4 класс, 4 четверть

вариант I

1. Выполните деление:

31 901 : 73 = 33 387 : 93 =

309 888 : 384 = 127 270 : 143 =

2. Выполните умножение:

213 * 307 = 836 * 167 =

589 * 372 = 430 * 132 =

3. Переведите:

5 часов 13 минут = … сек 1 тонн 3 центнеров 68 кг = … кг

1 км 43 метра = … дм 28 часов 42 мин = … мин

4. Решите задачу:

Отряд пионеров прошел 20 км. Это составляет четверть пути. Сколько должны пройти пионеры?

вариант II

1. Выполните деление:

25 296 : 68 = 6 279 : 13 =

111 948 : 114 = 173 990 : 274 =

2. Выполните умножение:

248 * 357 = 721 * 163 =

701 * 591 = 231 * 694 =

3. Переведите:

1 час 48 минут = … сек 4 тонн 8 центнеров 213 кг = … кг

2 км 483 метров = … дм 1 сутки 8 часов = … мин

4. Решите задачу:

Спортсмены пробежали 15 км. Это составляет треть пути. Сколько должны пробежать спортсмены?

вариант III

1. Выполните деление:

218 654 : 218 = 716 982 : 794 =

99 264 : 132 = 54 544 : 487 =

2. Выполните умножение:

478 * 306 = 404 * 715 =

213 * 372 = 397 * 702 =

3. Переведите:

3 часа 38 минут = … сек 13 тонн 7 центнеров 63 кг = … кг

16 км = … дм 4 часов 37 мин = … мин

4. Решите задачу:

Велосипедисты проехали 18 км. Это составляет пятую часть пути. Сколько должны проехать велосипедисты?

Самостоятельная работа по теме: « Итоговое повторение»

4 класс, 4 четверть

вариант I

1. Решите пример:

3 758 + 6 345 = 27 397 – 7 164 =

782 * 23 = 33 948 : 82 =

2. Найдите значения выражений:

3 000 : 60 – 250 : 50 =

( 213 173 – 19 403 ) : 2 – 31 * 73 =

3. Решите задачу:

Из пункта А одновременно в одном направлении выехали мотоциклист и велосипедист. Скорость мотоциклиста 72 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

вариант II

1. Решите пример:

7 165 + 18 448 = 55 103 – 731 =

694 * 36 = 18 144 : 567 =

2. Найдите значения выражений:

5 600 : 70 + 210 : 70 =

( 14 864 – 3 486 ) : 2 – 19 * 26 =

3. Решите задачу:

Из двух населенных пунктов одновременно навстречу друг другу выехали поезд и автомобиль. Скорость поезда 48 км/час, а автомобиля 72 км/час. Через какое время они встретятся, если расстояние между городами 360 км?

вариант III

1. Решите пример:

4 138 + 12 672 = 63 230 – 879 =

736 * 34 = 35 805 : 35 =

2. Найдите значения выражений:

4 200 : 60 – 490 : 70 =

( 114 378 – 21 366 ) : 2 – 31 * 72 =

3. Решите задачу:

Из одного города одновременно в разных направлениях выехали мотоциклист и велосипедист. Скорость автомобиля 65 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

Как записывать множители при подсчете столбиком

Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.

Пример 1

Например, чтобы вычислить и 71, 550·45 002 и 534 000·4 300, запишем такие столбики:

Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.

Как учить ребенка учиться

Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.

А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.

Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.

Что это такое?

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Повтори тему — деление в столбик, она очень полезная!

Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.

Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.

Что необходимо знать для умножения натуральных чисел столбиком?

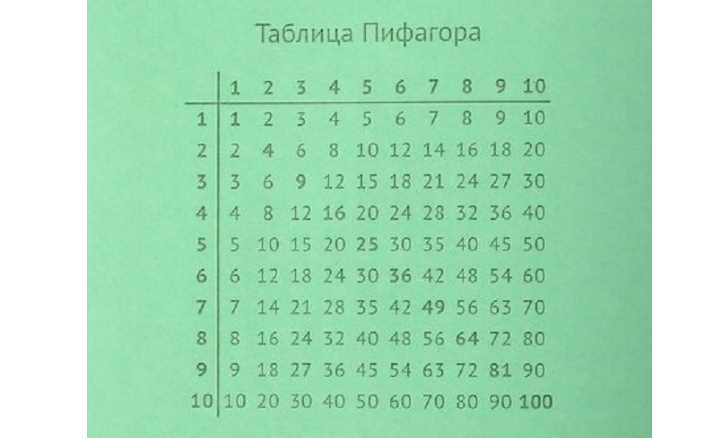
Промежуточные вычисления при умножении столбиком проводятся с использованием , поэтому ее желательно знать наизусть, чтобы не тратить время на поиск нужного результата.

Рано или поздно при умножении столбиком мы столкнемся с умножением однозначного натурального числа на нуль. В этом случае мы будем пользоваться : a·0=0, где a – произвольное натуральное число..

Рекомендуем разобраться с материалом статьи сложение столбиком. Это связано с тем, что на одном из этапов умножения в столбик приходится складывать промежуточные результаты (которые называют неполными произведениями), используя принцип сложения столбиком.

Также нам пригодятся навыки сравнения натуральных чисел.

Наконец, желательно вспомнить .

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Как объяснить ребенку умножение столбиком?

Как объяснить ребенку умножение столбиком?

Научить ребенка умножению — это реальная задача, но придется запастись терпением. Занятие должны быть регулярными, ведь только система поможет добиться желаемых результатов.

• Расскажите ребенку, что умножение — это повторение, сложение одинаковых чисел
• Напишите на листе бумаги примеры: 2+2+2+2+2 и 2х5
• Сделайте вместе с ребенком сравнение, как быстрее подсчитать сложением или умножением
• Чтобы закрепить эту полученную информацию, приведите примеры из жизни, но они должны быть не выдуманными. Например, к ребенку в гости идут 7 друзей. Для них готово лакомство — по 2 конфеты. Как быстрее подсчитать — сложением или умножением? Подсчитайте вместе с малышом и запишите на бумаге в виде примера: 7х2=14

Когда пройдет несколько занятий, таблица умножения будет выучена, тогда можно начинать объяснять ребенку умножение столбиком двухзначных и трехзначных чисел.

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041.