Таблица умножения до 20 и до 100

Таблица сложения до 20

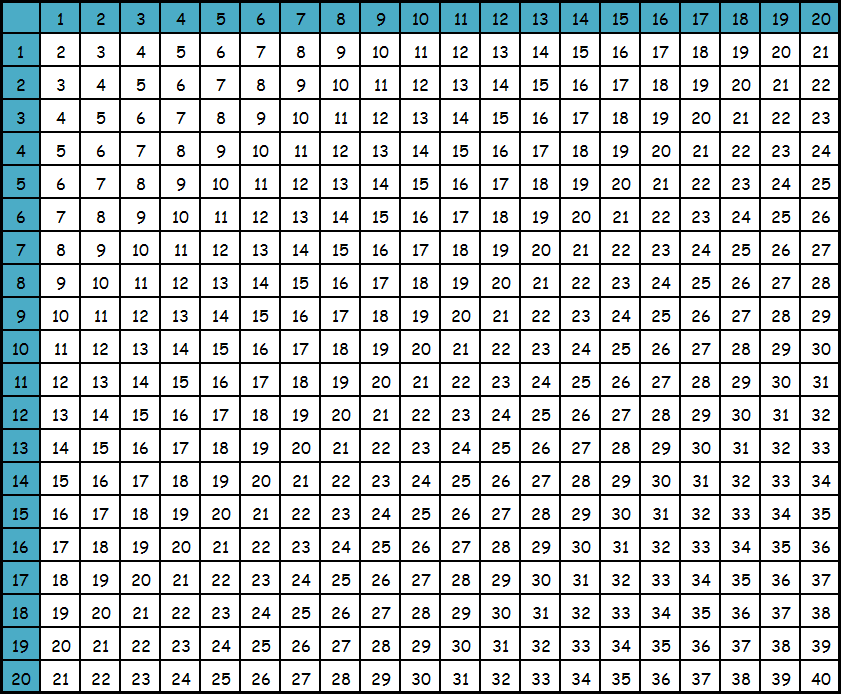
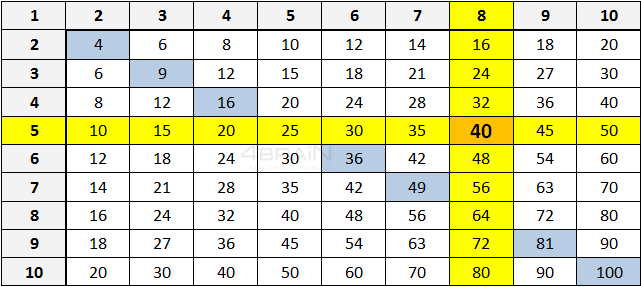
Сложим 3 и 4. Находим число 3 по горизонтали и число 4 по вертикали. Мысленно проводим линии до места пересечения. Это и есть искомое значение. Нетрудно заметить, что если мы поменяем местами значения и отыщем по горизонтали 4, а по вертикали — 3, то также в ячейке будет 7.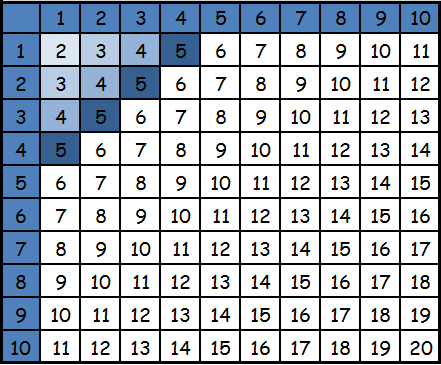

Отсюда вытекает одно из свойств, справедливых для суммы чисел. Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6. Далее все аналогично. Для больших чисел обычно таблицы не составляются. Таблица вычитания. Этой же таблицей можно пользоваться и для операции вычитания. В этом случае производим обратные действия. В самой таблице находим значение, из которого нужно вычесть число. Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.

Для ознакомления также ниже представлены более старые варинты таблицы.
 

Таблицы сложения значительно упрощают повседневный счет, поэтому много лет назад люди начали их использовать и некоторые из них мы можем видеть в сохранившихся книгах. Например, так выглядела таблица сложения в книге «Арифметика» Магницкого Л. Ф. 1703 года издания.

(на картинке фото фрагмента из оцифрованной версии книги, саму книгу найти было достаточно сложно, поэтому использована сканированная версия, которая есть в широком доступе) Так выглядит эта таблица в воспроизведении (переиздании) той же книги, сделанном в 1914 году под редакцией П. Баранова: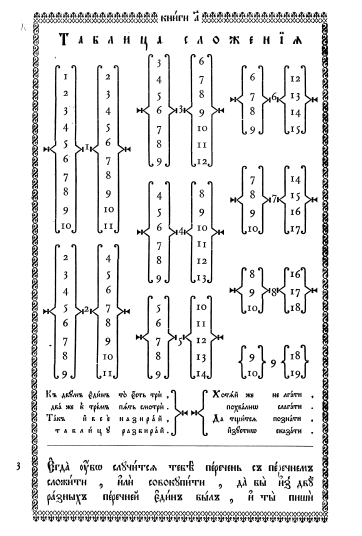
(на картинке как раз фотография тоже сканированной версии переиздания 1914 года).

Таблица продуктов для диеты №2

Таблица деления чисел, на 2,3,4,5,6,7,8,9 ПРОДУКТ	РАЗРЕШЕНО	ЗАПРЕЩЕНО
Супы	На овощном или втором мясном бульоне с добавлением круп	Рассольник, щи, борщ, солянка, наваристые мясные бульоны
Яйца	В любом виде, кроме приготовленных вкрутую	Сваренные вкрутую
Рыба	Вареная без кожи, паровые котлеты, нежирные сорта	Жареная, консервированная, соленая, вяленая, икра
Мясо, птица	Куриное филе, телятина, индейка, кролик, язык, печень, колбаса без жира, молочные сосиски	Жирные и жилистые сорта, баранина, дичь, копчености, сало
Хлеб и выпечка	Подсушенный или вчерашний хлеб, сухое печенье, несдобные изделия	Свежие сдобные изделия, слоеное тесто, ржаной хлеб, блины всех разновидностей
Молочные продукты	Некислые творог, кефир и сметана, сыр нейтрального вкуса	Молоко
Крупы	Рис, овсянка, макароны, вермишель	Гречка, перловка, все бобовые и кукуруза
Овощи	Термически обработанные цветная капуста, брокколи, свекла, морковь, картофель, кабачки, тыква	Огурцы, грибы, белокочанная капуста, огурцы, репа
Фрукты и ягоды	Яблоки, цитрусовые, бананы, вишня, черешня	Груши, крыжовник, инжир, смородина, малина, виноград
Напитки	Чай, кофе, какао, отвар шиповника	Газировка, алкоголь
Десерты	Зефир, пастила, мармелад, варенье, джем	Мороженое, халва, сладкая сдоба

Составить щадящий рацион по данной таблице не составит особого труда.

Варианты меню на день для стола №2 (на выбор):

Завтрак: овсяная каша/омлет на пару/бутерброд с сыром + напиток.

Обед: овощной суп + картофельное пюре с отварной рыбой без кожи/нежирный бульон с сухариками + куриное филе с рисом.

Полдник: творог/фруктовое желе/чай с печеньем.

Ужин: постная говядина + запеченные в духовке овощи/паровые котлеты + гречка/лосось на пару + брокколи.

На ночь: стакан кефира, простокваши или натурального йогурта без добавок.

pixabay.com &nbsp/&nbspRitaE

Диета №2 не подразумевает значительных ограничений в еде, поэтому переносится легко и помогает быстро восстановиться.

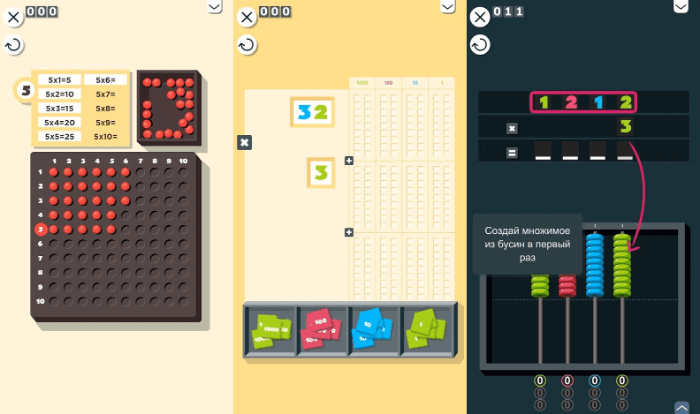
Multiplication with Ibbleobble

Это приложение поможет ребенку научиться быстрее перемножать числа, навык, который пригодится не только на уроках и экзаменах, но и за стенами школы. Вопросы базируются на таблице умножения, которую дети осваивают в младших классах.

В самом начале нужно выбрать из нескольких симпатичных животных виртуального друга, с которым он будет играть. После этого указывается уровень сложности. На легком уровне нет никаких ограничений по времени. На среднем и тяжелом уровне время на решение задач ограничено.

В каждом задании представлена задача на умножение, а игроку нужно выбрать правильный ответ из трех вариантов. В процессе игры дети собирают «вкусняшки» для своего персонажа. Например, для мистера Мыши это будут кусочки сыра.

Главный недостаток приложения заключается в том, что оно не помогает учить таблицу умножения. Оно рассчитано на детей, которые ее уже знают. Приложение же помогает только научиться умножать быстрее.

Доступно только для iPhone.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Вы здесь

Таблица умножения и деления

Файлы: 

Вложение	Размер
Таблица умножения и деления, картинка с пояснением	74.46 КБ
Таблица умножения и деления	105.44 КБ
Таблица умножения и деления без ответов	19.53 КБ

Чтобы скачать и рапсечатать таблицу умножения и деления, используйте ссылки выше или нажмите правую кнопку мышки над картинками ниже и выберите «сохранить картинку как».

Таблица умножения и деления без ответов.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Связь умножения и сложения

Ворчун любит поворчать, потому что ему не нравится, что гномов окружают одинаковые вещи.

Надо считать одинаковое количество карманов на одинаковых куртках, пальто или вычислять сложением количество деревьев в лесу. Ворчун добывает гранит. Этим камнем облицованы набережные в городах, отделаны стены домов и станций метро.

Чтобы посчитать, сколько разных цветов гранита нашел, Ворчун к трем прибавляет три четыре раза.

Получается пример:

Гном собирает коллекцию камней и минералов. В ряду четыре штуки. Посчитайте сколько ископаемых в семи рядах.

Семь раз возьмите по 4 камня. Получается длинная запись

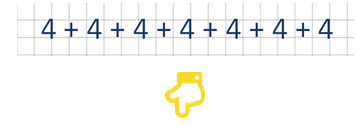
А если рядов будет не семь, а например 60. Надо 60 раз складывать? Обязательно собьемся. В реальной жизни в магазине товар исчисляется сотнями и тысячами.

Посмотрите на розовый известняк из кладовых Земли. Из него сделали много плиток для строительства домов и дорог.

Ребята, Ворчун ворчит, а Весельчак расскажет про новое волшебное действие, которое помогает пересчитывать большие количества предметов.

Люди придумали, как сделать запись короче и вычислять быстрее. Они решили назвать это действие умножением. Получается, что операции сложения и умножения тесно связаны между собой. Умножение – особый случай сложения, когда одно число складывается много-много раз. Мы имеем дело уже не с действием сложения, а умножением.

Записывается пример так: на первое место поставьте число, которое повторяется, потом знак умножения – точку. Иногда вместо точки ставят крестик — x. На клавиатуре компьютера или смартфона знак изображают как звездочку *. На второе место запишите то число, сколько раз оно повторяется.

Давайте посмотрим, как это выглядит в жизни. Допустим, у нас есть пять книг, в каждой из них по 100 страниц.

Сколько всего страниц? Видите – здесь идет повторение одного и того же числа по 100 страниц. Поэтому надо все эти страницы сложить.

Конечно, это легче сделать умножением. Сначала напишите сто, затем точку. Посмотрите сколько раз надо взять по сто. Пять раз.

Рассмотрим другой случай. Сколько будет стоить 4 мороженых по 30 рублей за каждое?

Мы будем платить за первое мороженое 30 рублей, за второе 30, за третье 30 и за четвертое столько же.

Заменим умножение сложением: получается, что повторяется 30 рублей. Ставим на первое место 30, дальше точка и четверка.

4 раза заплатим за эти мороженые по тридцать рублей.

Решим задачу на умножение.

Бабушка сварила на зиму 6 банок варенья по 3 литра в каждой. Сколько варенья сварила бабушка?

Когда решаете задачу, всегда представляйте ее условие.

3 литра – количество варенья в банке

6 – сколько раз мы берем по шесть

3 литра ∙ 6 раз = 18 литров

Прочитайте решение: по три взять шесть раз получится восемнадцать. Или три умножить на шесть получится восемнадцать.

Таблицу умножения нужно знать наизусть. Но как быть, если еще не выучили? Вычислите умножение сложением:

Например, нужно 30 х 4. Значит надо сложить 30 четыре раза.

Фраза «умножить число пять на число три» или же «пятью три» означает «пять плюс пять, плюс пять».

Это кратчайший путь для ситуаций, когда складывается много раз одно и то же число.

В записи операции умножения первое число называется первый множитель, второе число — второй множитель, а результат умножения называется произведением.

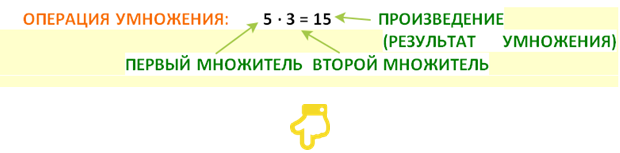
Запомните друзья, умножение – это действие, которое увеличивает число. Берем маленькое число несколько раз, получается большое число

Это важно помнить

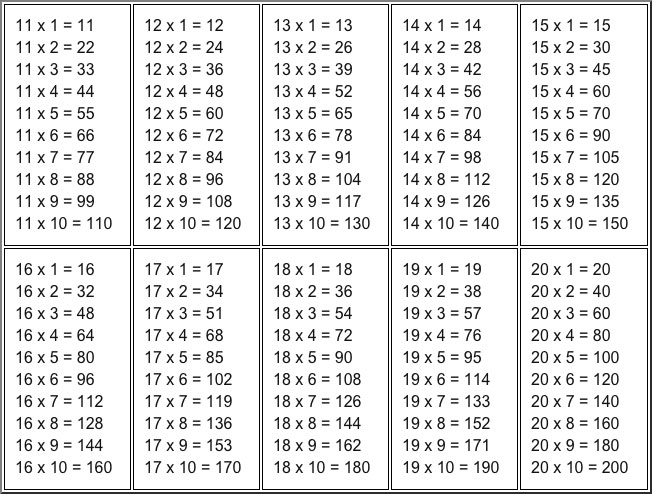
Таблица умножения в стандартном виде от 10 до 20

11 х 1 = 11 11 х 2 = 22 11 х 3 = 33 11 х 4 = 44 11 х 5 = 55 11 х 6 = 66 11 х 7 = 77 11 х 8 = 88 11 х 9 = 99 11 х 10 = 110	12 х 1 = 12 12 х 2 = 24 12 х 3 = 36 12 х 4 = 48 12 х 5 = 60 12 х 6 = 72 12 х 7 = 84 12 х 8 = 96 12 х 9 = 108 12 х 10 = 120	13 х 1 = 13 13 х 2 = 26 13 х 3 = 39 13 х 4 = 52 13 х 5 = 65 13 х 6 = 78 13 х 7 = 91 13 х 8 = 104 13 х 9 = 117 13 х 10 = 130	14 х 1 = 14 14 х 2 = 28 14 х 3 = 42 14 х 4 = 56 14 х 5 = 70 14 х 6 = 84 14 х 7 = 98 14 х 8 = 112 14 х 9 = 126 14 х 10 = 140	15 х 1 = 15 15 х 2 = 30 15 х 3 = 45 15 х 4 = 60 15 х 5 = 70 15 х 6 = 90 15 х 7 = 105 15 х 8 = 120 15 х 9 = 135 15 х 10 = 150
16 х 1 = 16 16 х 2 = 32 16 х 3 = 48 16 х 4 = 64 16 х 5 = 80 16 х 6 = 96 16 х 7 = 112 16 х 8 = 128 16 х 9 = 144 16 х 10 = 160	17 х 1 = 17 17 х 2 = 34 17 х 3 = 51 17 х 4 = 68 17 х 5 = 85 17 х 6 = 102 17 х 7 = 119 17 х 8 = 136 17 х 9 = 153 17 х 10 = 170	18 х 1 = 18 18 х 2 = 36 18 х 3 = 54 18 х 4 = 72 18 х 5 = 90 18 х 6 = 108 18 х 7 = 126 18 х 8 = 144 18 х 9 = 162 18 х 10 = 180	19 х 1 = 19 19 х 2 = 38 19 х 3 = 57 19 х 4 = 76 19 х 5 = 95 19 х 6 = 114 19 х 7 = 133 19 х 8 = 152 19 х 9 = 171 19 х 10 = 190	20 х 1 = 20 20 х 2 = 40 20 х 3 = 60 20 х 4 = 80 20 х 5 = 100 20 х 6 = 120 20 х 7 = 140 20 х 8 = 160 20 х 9 = 180 20 х 10 = 200

Тренажер Таблица умножения и устный счет

Для того чтобы быстро считать в уме необходимо постоянно тренироваться. И тренажер устного счета как раз окажет вам помощь. Вначале вам будут задаваться простые примеры, например 2 + 3, но чем больше правильных ответов вы дадите, тем сложнее примеры будут предлагаться.

Следующий тренажер посвящен таблице умножения и деления. Многие недооценивают значения таблицы умножения, считают, что достаточно иметь калькулятор. Но из учебной практики видно, что те школьники, которые знают таблицу умножения на память, намного быстрее и легче осваивают математику и другие точные науки. Поэтому вначале выучите таблицу умножения, а потом с помощью тренажера повторяйте, чтобы всю таблицу умножения знать как 2*2=4.

5+ игр для быстрого запоминания таблицы умножения

Чтобы быстро выучить таблицу умножения, ребенку в возрасте 8-10 лет — а именно столько ему во 2-4 классе, когда в программе появляется умножение — стоит подобрать игру по вкусу. Так процесс пойдет намного эффективнее, чем в случае простой зубрежки.

Вот перечень наиболее распространенных и интересных вариантов игрового обучения:

Карточки

Их можно распечатать самостоятельно, а можно приобрести практически в любом детском магазине — настолько эта игра известна и популярна. Набор включает все комбинации множителей из таблицы умножения с ответами на оборотной стороне.

Чтобы быстро выучить их, играть предлагается следующим образом:

1. Игрок тянет пример
2. В случае правильного ответа карточка отправляется в «отбой»
3. В случае неправильного — возвращается в колоду

Повторять перечисленные шаги следует до тех пор, пока в основной колоде не останется карт. За счет того, что сложные примеры возвращаются в стопку и встречаются снова и снова, они запоминаются лучше и прочнее.

Чтобы выучить всю таблицу умножения максимально быстро, попробуйте устроить игру на время. Ребята, занимающиеся во 2-3 классе, наверняка будут в восторге от такой викторины.

Вам на помощь придут развивающие компьютерные игры

Стихотворные примеры

Разучите с ребенком самые простые рифмующиеся примеры из таблицы умножения: пятью пять, шестью шесть и т.д. А можно сразу взять на вооружение стихотворный разбор всей таблицы — например, книгу Андрея Усачева «Таблица умножения в стихах».

Яркие иллюстрации и интересные короткие стишки превратят зубрежку в увлекательную игру. Чтобы быстро выучить таблицу во 2 или 3 классе, такой способ подойдет как нельзя лучше.

Счет на пальцах

Любознательным детям втянуться в обучение наверняка поможет один наглядный прием-хитрость умножения на девять.

Рассмотрим его на примере пятью девять:

1. Смотрим на собственные ладошки
2. Отсчитываем пятый пальчик слева (как показатель множителя 5)
3. Считаем количество пальцев слева от «множителя» — это десятки (в данном примере их будет четыре)
4. Считаем количество пальчиков справа от пятого — это единицы (в данном примере их пять)

Итогом будет число 45 — ответ на пример из таблицы умножения. Такой подход работает для любых умножений на девять — попробуйте сами.

Ни в коем случае не критикуйте ребенка за неудачи

Использование игрушек или наглядных примеров

Чтобы быстро выучить принципы умножения на 2 и 3 по таблице умножения, можно использовать в качестве подспорья в игре практически что угодно: игрушки, предметы на улице, людей, животных и т.д.

Выберите такой пример, который более знаком и привычен вашему ребенку. Выстраивайте в ряд по два и три игрушки и считайте их. Потом объясните ребенку принцип сокращения процесса подсчета с помощью умножения.

Мобильные или онлайн-игры на изучение таблицы умножения

В сети существует бесчисленное количество разных игр, направленных на то, чтобы быстро выучить таблицу умножения, играя онлайн. Подберите вместе с ребенком увлекательную и яркую игру и предоставьте ему развлекаться — а после проверьте успехи.

Если вас заботит неконтролируемое пребывание ребенка в интернете, выберите игру, которую можно бесплатно скачать, и используйте ее, чтобы быстро выучить таблицу умножения.

Есть много способов привлечь внимание ребенка

Морской бой

Этот игровой способ отлично подходит для закрепления уже имеющихся знаний. Запишите поля «морского боя» цифрами с обеих сторон и установите, что для атаки сектора нужно назвать результат умножения соответствующих чисел.

Такая несложная и увлекательная игра отлично тренирует память и скорость умножения. Конечно, чтобы быстро выучить таблицу умножения во 2 классе, игра нужна не всегда.

Некоторые детки, особенно если им повезло со школьными преподавателями и вообще отношением к учебе, с интересом будут постигать принципы математических примеров и без игр.

В этом случае используйте системный пошаговый подход к обучению:

1. Объясните принцип умножения на единицу и десятку
2. Освойте удвоение
3. Разберите принцип неизменности результата от перестановки множителей
4. Выучите квадраты чисел
5. Последовательно переходите к изучению умножения на 3, 4, 5 и т.д.

Настройтесь на позитивный лад, и результат не заставит себя долго ждать

Даже в такой подход можно добавить игровой элемент, помечая разными цветами уже заученные области. Финальной целью игры будет очищение поля.

Запоминание таблицы умножения — одна из первых ступеней в обучении ребенка математике, одна из важнейших основ. 

Мы уверены, что вы выберете оптимальный подход и успешно изучите все тонкости умножения чисел. Больше наглядного материала по игровому изучению таблицы вы сможете найти в этом видео: