Порядок действий в математике

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

1% = 1/100 = 0,01

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Быстрая напоминалка:

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Ответ: 5,4 = 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

Как решаем:

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Цикл Пока

Данный цикл предназначен для осуществления повторений, пока выполняется условие. Синтаксис цикла выглядит так:

Для выполнения очередного повторения Логическое выражение должно возвращать значение Истина. Это работает следующим образом:

1. Вычисляем значение Логического выражения. Если оно Ложь, цикл завершается. Если Истина:
2. Выполняем операторы цикла;
3. Возвращаемся на п. 1.

Пример 1. При помощи сообщения вывести пользователю цифры от 1 до 10.

Таким образом в цикле Пока нам необходимо не только выполнить требуемое действие, но и изменить переменную участвующую в проверке его условия. Если забыть это сделать, можно получить бесконечный цикл, который приведет к зависанию системы.

Пример 2. А теперь только не четные, в интервале от 1 до 100, в обратном порядке.

В примере используется операция %. Она получает остаток от деления одного числа на другое.

При помощи цикла Пока можно обойти массив или любую другую коллекцию в обратном порядке. Это необходимо не часто, но реализовать такой механизм при помощи других циклов проблематично. Рассмотрим такой механизм в примере 3.

Также цикл Пока часто используется для обхода выборки из результата запроса. У выборки для этого есть специальный метод Следующий(). Он осуществляет переход на следующую строку и возвращает Истина, если такая строка есть. Если же следующая строка отсутствует в выборке, метод возвращает Ложь. Нельзя забывать, что работу с запросом можно осуществлять только в серверной процедуре (или функции).

Пример 4. При помощи запроса выбрать всех пользователей, кроме недействительных. Обойти выборку циклом Пока.

Как посчитать проценты, разделив число на 10

Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.

Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.

Пример

Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.

В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.

Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.

Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.

В любом случае такими крупными числами оперировать довольно просто.

Эта сложная наука – математика

Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.

Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.

Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.

Простые задачи на уменьшение числа на несколько единиц

1. В букете 5 розовых пионов, а белых на 3 пиона меньше. Сколько белых пионов в букете?
2. На первом этаже расположено 6 квартир, а на втором этаже на 4 квартиры меньше. Сколько квартир на втором этаже?
3. Костя из 10 выстрелов попал в цель 8 раз, а Толя на 2 раза меньше. Сколько раз в мишень попал Толя?
4. В столовой были 4 кастрюли с кашей, а с компотом на одну кастрюлю меньше. Сколько кастрюль с компотом было в столовой?
5. Собрали 8 кг ягод малины, а ягод смородины на 3 кг меньше. Сколько килограммов ягод смородины собрали?
6. У бабушки Нины 6 горшков красной герани, а белой на 2 горшка меньше. Сколько горшков белой герани у бабушки Нины?
7. На крыше сидит 9 воробьёв, а голубей на 5 птиц меньше. Сколько голубей сидит на крыше?
8. Перед домом стоит 7 машин, а мотоциклов на 5 меньше. Сколько мотоциклов стоит перед домом?
9. Длина клумбы 5 м, а её ширина на 3 м меньше. Какова ширина клумбы?
10. Пока хлеб был мягким, он весил 9 кг, а когда зачерствел, вес его уменьшился на 2 кг. Узнай вес чёрствого хлеба.
11. Вася поймал 7 пескарей, а Олег на 3 пескаря меньше Сколько пескарей поймал Олег?
12. В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе?
13. В кружке рисования занимаются 9 детей, а в кружке бальных танцев на 3 человека меньше. Сколько детей занимаются в кружке бальных танцев?
14. Детёныш кобры находится в яйце 10 недель, а детёныш ужа на 4 недели меньше. Сколько недель находится в яйце детёныш ужа?
15. Масса яйца сороки 10 г, а масса яйца кукушки на 7 г меньше. Определи массу яйца кукушки.
16. В доме 7 кресел, а диванов на 4 меньше. Сколько диванов в доме?
17. Гриша съел 3 орешка, а Слава на 1 орешек меньше. Сколько орешков съел Слава?
18. Около дома растёт 10 берёз, а дубов на 6 меньше. Сколько дубов растёт около дома?
19. Творожный сырок стоит 6 руб., а глазированный на 2 руб. дешевле. Сколько стоит глазированный сырок?
20. Папа купил 9 кг картофеля, а лука на 6 кг меньше. Сколько килограммов лука купил папа?
21. Около школы посадили 7 кустов сирени, а жасмина на 3 куста меньше. Сколько кустов жасмина посадили?
22. Никита собрал 9 еловых шишек, а сосновых на 5 шишек меньше. Сколько сосновых шишек собрал Никита?

Простые задачи на сложение в одно действие

1. В классе в кружке рисования занимались 6 мальчиков и 2 девочки.Сколько всего детей занимались рисованием?
2. К новогоднему празднику Оля отправила 4 открытки с поздравлениями, а Маша 6 открыток. Сколько всего открыток отправили девочки?
3. На стройку привезли 4 машины гравия и 6 машин песка. Сколько всего машин строительного материала привезли?
4. В одном альбоме 4 открытки с цветами, а в другом 5 открыток с животными. Сколько всего открыток в двух альбомах?
5. У мамы были 3 розы. Ей подарили ещё 5 роз. Сколько всего роз стало у мамы?
6. У Пети были 3 видеокассеты с мультфильмами. Ему купили ещё 6 видеокассет. Сколько всего видеокассет стало у Пети?
7. На даче росли 3 куста крыжовника. Посадили ещё 5 кустов крыжовника. Сколько всего кустов крыжовника стало на даче?
8. За первую четверть ученик исписал 3 синих стержня, а за вторую четверть 2 синих стержня. Сколько всего синих стержней исписал ученик за две четверти?
9. За первый час турист прошёл 5 км, за второй 4 км. Сколько всего километров турист прошёл за 2 ч пути?
10. Зина купила 4 книги со сказками и 5 книг со стихами. Сколько всего книг купила Зина?
11. На стол поставили 2 вазы и 5 подносов. Сколько всего предметов поставили на стол?
12. Во дворе живут 3 собаки и 4 кота. Сколько всего животных живут во дворе?
13. На ветке сидело 5 воробьёв и 2 синички. Сколько птиц сидело на ветке?
14. На лугу паслось 6 коз и 2 лошади. Сколько животных было на лугу?
15. Днём белка принесла в дупло 6 грибов, а вечером 3 гриба. Сколько грибов стало в дупле?
16. На полке стоит 5 толстых книг с рассказами и одна тонкая книга со сказками. Сколько всего книг стоит на полке?
17. Аня вымыла 5 тарелок, а Миша вымыл 4 тарелки. Сколько всего тарелок вымыли дети?
18. В саду растут 2 саженца груши и 5 саженцев вишни. Сколько всего саженцев растёт в саду?
19. Аня купила 2 пирожка с капустой и 3 пирожка с повидлом. Сколько всего пирожков купила Аня?
20. В первую неделю июля Гриша искупался 5 раз, во вторую неделю 4 раза. Сколько раз Гриша искупался в реке за две недели?

Сложение и умножение вероятностей

Немного теории:

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

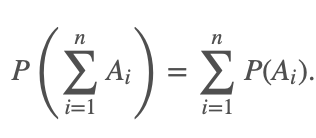
Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство: 

P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

Как рассуждаем:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Задачи на понятие «столько же»

1. У Коли 4 машинки, у Дениса столько же. Сколько всего машинок у мальчиков?
2. В одном стручке 5 горошин и в другом столько же. Сколько горошин в двух стручках?
3. На одной ветке 3 груши и на другой столько же. Сколько всего груш на двух ветках?
4. У папы 2 брата и столько же сестёр. Сколько всего братьев и сестёр у папы?
5. В конфетнице лежали 4 карамельки и столько же шоколадных конфет. Сколько всего конфет лежало в конфетнице?
6. У кошки 5 белых котят и столько же серых котят. Сколько всего котят у кошки?
7. На доске лежало 3 куска фиолетового мела и столько же кусков жёлтого. Сколько всего кусков мела лежало на доске?
8. На столе стояли 3 чашки и столько же блюдец. Сколько всего предметов стояло на столе?
9. В секции плавания занимались 4 девочки и столько же мальчиков. Сколько всего детей занимались в секции плавания?
10. У школы росли 3 берёзы. Дети посадили ещё столько же берёз. Сколько всего берёз стало у школы?
11. Кате на день рождения подарили 2 куклы, 6 зайчиков, а воздушных шариков столько, сколько кукол и зайчиков вместе. Сколько воздушных шариков подарили Кате?
12. На опушке леса росло 5 клёнов и 4 тополя, а сосен росло столько, сколько клёнов и тополей вместе. Сколько сосен росло на опушке леса?
13. Костя исписал за первую четверть 3 тетради, за вторую четверть 4 тетради, а за третью исписал тетрадей столько, сколько за первую и вторую четверти вместе. Сколько тетрадей исписал Костя за третью четверть? 
14. В букете 5 одуванчиков, 4 лютика, а васильков столько, сколько одуванчиков и лютиков вместе. Сколько васильков в букете?
15. На стоянке стояло 3 жёлтые машины, 7 зелёных, а красных машин столько, сколько жёлтых и зелёных вместе. Сколько красных машин стояло на стоянке?
16. Серёжа решил 2 задачи утром, 3 задачи днём, а вечером решил задач столько, сколько утром и днём вместе. Сколько задач решил Серёжа вечером?
17. Маше 6 лет, Кате 4 года, а Толе столько лет, сколько Маше и Кате вместе. Сколько лет Толе?
18. В первой группе 6 девочек, во второй группе 2 девочки, а в третьей столько, сколько в первой и второй группах вместе. Сколько девочек в третьей группе?
19. На первой клумбе 4 тюльпана, на второй 3 тюльпана, а на третьей клумбе столько, сколько на первой и второй клумбах вместе. Сколько тюльпанов растёт на третьей клумбе?
20. У рыжей кошки 4 котёнка, у серой 3, а у белой столько, сколько у рыжей и серой вместе. сколько котят у белой кошки?

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Свойства вероятности:

• Вероятность достоверного события равна единице.
• Вероятность невозможного события равна нулю.
• Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

0 ≤ P(A) ≤ 1.

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Как рассуждаем:

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

P = 0/15 = 0

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное. 

Ответ: 0.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Как рассуждаем:

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m). 

Следовательно:

Ответ: 0,25.

Как посчитать проценты, разделив число на 100

Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.

Пример 1

Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.

Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.

Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.

Умножьте 4,58 на 7, и вы получите 32,06 рубля.

Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.

Пример 2

Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.

Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.

Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.

100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.