34 примера человеческой глупости, с которых ни в коем случае не стоит брать пример

Введение в пример

Окей, со статьей легко: это сравнительно небольшая форма. В ней можно донести мысль на одном, двух или трех примерах.

А что если мы пишем не статью, а серию статей? Или, еще сложнее, — книгу? Каждый раз давать примеры об одном и том же будет скучно. И по смыслу это не всегда получится: разные темы будут требовать разных ситуаций. Тогда принцип единства примера не подходит, нужно действовать иначе.

Если у вас примеры из разных ситуаций, сделайте так, чтобы читатель смог мысленно к ним подготовиться. Дайте ему сигнал, о чем сейчас пойдет речь. Не кидайте в него примеры без предупреждения. Вот как это будет работать в статье о спорте. Смотрите на порядок слов:

Нет	Да
…у вас будут силы заниматься спортом по утрам. Накатите стакан водки, если собираетесь на пробежку. Или покурите, если вместо пробежки вы выбрали тяжелую атлетику.	…у вас будут силы заниматься спортом по утрам. Если вы выбрали пробежку, накатите с утра стакан водки. А если вы выбрали тяжелую атлетику — выкурите одну сигарету.

В примере слева автор сначала дает совет, потом объясняет ситуацию. В примере справа сначала готовит читателя к ситуации и только потом дает совет. У читателя есть возможность вспомнить всё, что он уже знает о беге, прежде чем добавлять к этому знанию что-то новое.

Кажется, что это незначительная разница. Но вы ее прочувствуете, когда у вас будет по пять примеров на странице. Если не вводить читателя в новый пример, то он быстро устанет.

Вводить в пример можно одним словом, предложением или даже абзацем, в зависимости от задачи и сложности самого примера:

Когда вы бежите…

Например, когда вы бежите…

Представьте, что вы бежите по парку.

Чтобы понять эту идею, давайте проведем мысленный эксперимент. Вспомните парк возле своего дома. Представьте, что вы по нему бежите.

Такая подготовка дает читателю время вспомнить всё нужное.

Готовьте читателя к новому примеру.Не бросайте в него нового без подготовки.

На примере книги

У нас с Людой была такая проблема в книге «Пиши, сокращай». Каждый наш параграф — это немного теории и много примеров. Все примеры должны быть разными, в этом смысл книги. И мы обнаружили, что если читателя не вводить в примеры, то текст получится слишком сложным. Голова взрывалась. Вот фрагмент из первой же главы до редактуры:

Информационный стиль ставит правду на первое место, даже если она неудобная. Даже если все вокруг просят сгладить углы.

Сглаженные углы	Неудобная правда
Вследствие стечения обстоятельств и изменения экономической конъюнктуры структура расходов на возведение данных объектов инфраструктуры не соответствовала рыночным условиям, вследствие чего мы вынуждены рассмотреть вопрос об увеличении бюджета.	Мы не заложили в смете рост цен на стройматериалы. Теперь нам не хватает денег, чтобы постелить крышу. Чтобы открыть эту школу в сентябре, нам нужно еще 2,5 миллиона.

Пример о недостроенной школе здесь внезапный: раньше в главе его не было, позже он не встречается. Он взят здесь локально, чтобы доказать мысль. Но если к нему не подготовить, он не «заходит». Чтобы «зашел», достаточно было одним предложением подготовить читателя:

Информационный стиль ставит правду на первое место, даже если она неудобная. Даже если все вокруг просят сгладить углы. Представьте, что мэрия отчитывается о строительстве школы:

Сглаженные углы	Неудобная правда
Вследствие стечения обстоятельств и изменения экономической конъюнктуры структура расходов на возведение данных объектов инфраструктуры не соответствовала рыночным условиям, вследствие чего мы вынуждены рассмотреть вопрос об увеличении бюджета.	Мы не заложили в смете рост цен на стройматериалы. Теперь нам не хватает денег, чтобы постелить крышу. Чтобы открыть эту школу в сентябре, нам нужно еще 2,5 миллиона.

Одно предложение вытягивает весь пример. Теперь нестрашно хоть всю главу обставить новыми примерами: если читателя готовить к каждому из них, он не устанет.

Зачем нужны примеры

Вот вы пишете книгу, рассылку или статью. У вас есть абстрактная идея, которую вы хотите донести до читателя. Представьте, что вы пишете статью о спорте для людей, которые работают за компьютером. Ваша абстрактная идея — надо заниматься спортом хотя бы три раза в неделю.

Это абстрактная идея.

В этой абстрактной идее пока что не заложено ни то, каким конкретно спортом следует заниматься; ни как это делать; ни как оторвать задницу от стула; ни что делать после первого растяжения. Просто абстрактный призыв: «Занимайся спортом». Подобных статей миллион, и все они — говно.

Чтобы статья не была говном, вам нужно наполнить абстрактную идею реальностью:

рассказать, каким именно спортом стоит начать заниматься, если ты все время занят за компом;

привести пример графика, который не будет мешать работе — очевидно же, что у человека в жизни другие приоритеты;

рассказать, кто и как научился совмещать компьютер и спорт; как это у него работает; от чего он отказался;

Представьте, что вы печатаете свою абстрактную идею на 3Д-принтере: загружаете модель, подаете материал, получаете физический предмет. Это то, как работают примеры: они делают ваш текст реальным и осязаемым. Теория — это то, чему вы хотите научить. Примеры — это то, благодаря чему люди научатся.

К любой теории приведите пример

Как правильно научить ребёнка решать задачи

Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.   

1. Внимательно читаем условия  

Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.

Особую сложность представляют задачи с косвенным вопросом, например:

«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.        

2. Делаем описание задачи

В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 

Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.  

Формы краткой записи условий задач / shkola4nm.ru‍

3. Выбор способа решения

Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно. 

Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых. 

Ребёнок должен знать способы получения неизвестных данных из двух известных:

• слагаемое = сумма − слагаемое
• вычитаемое = уменьшаемое − разность
• уменьшаемое = вычитаемое + разность
• множитель = произведение ÷ множитель
• делитель = делимое ÷ частное
• делимое = делитель × частное

После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем. 

4. Формулировка ответа

Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.

Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс‍

Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.   

5. Закрепление результата

Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.

Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов. 

В нашей онлайн-школе, помимо уроков, ученики могут закреплять  свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения. 

Метаграммы по русскому языку для школьников

Метаграммы по русскому языку для школьников

Метаграммы по русскому языку для школьников:

Был день, стала ночь:
1. день — сень — сель — соль — ноль — ночь;
2. день — пень — пена — вена — вина — виза — ваза — фаза — фара — кара — кора — кожа — ложа — ложь — рожь — роль — ноль — ночь.

От мрака — к свету:
Мрак — брак — брус — трус — трос — трон — урон — урок — срок — сток — стон — стан — стая — свая — сват — свет

Как река стала лужей, а затем превратилась в море:
река — рука — лука — лужа — ложа — лоза — поза — пора — гора — горе — море.

Нога может стать рукой:
Нога — нота — рота — роза — лоза — луза — муза — мука — рука

А Луна Марсом:
Луна — лупа — лапа — лама — рама — раса — роса — коса — кора — гора — горе — море — морс — Марс

Дым может стать паром, а пар превратиться в лед:
1.Дым — дом — сом — сор — бор — бар — пар — пир — пик — лик — лак — лад — лед

Как из ржи муку получить:
рожь — ложь — ложа — лужа — лука — мука

Как суп попал в рот:
суп — сук — сок — сом — ром — рот

Как тесто превращается в булку:
1.тесто — место — месть — масть — пасть — паста — каста — каска — качка — пачка — палка — балка — белка — булка
2.тесто — место — месть — масть — пасть — паста — каста — карта — парта — парка — барка — бурка — булка;

Волк в тигра:
волк — полк — пола — пора — пара — пава — лава — лавр — ливр — литр — титр — тигр;

Барс в лису:
барс — фарс — фара — пара — папа — лапа — липа — лиса;

Коза то в лань, то в коня, то в волка:
1. коза — роза — риза — виза — вина — вена — пена — пень — день — лень — лань
2. коза — кора — корь — конь
3. коза — поза — пола — полк — волк;

Паук в муху:
паук — парк — пара — кара — Кура — купа — лупа — лука — мука — муха;

Кошка в мышку, а мышка в мишку:
кошка — мошка — мышка — мишка;

Ворона в корову:
ворона — корона — корова;

Сойка в чайку:
сойка — сайка — чайка;

Гриб в гнома:
гриб — грим — гром — гном;

Жаба в рыбу:
жаба — раба — рыба;

Рак в кита:
рак — рок — сок — сом — ком — кот — кит;

Муха в слона:
муха — мура — тура — тара — ката кара — каре — кафе — кафр — каюр — каюк — крюк — крок — срок — сток — стон — слон.

Коза смотрит на репу, но не знает, как до нее добраться:
коза — лоза — луза — муза — мука — рука — река — репа

Душа переселяется в тело:
душа — суша — сушь — суть — сеть — сень — сено — село — тело

Враг становится другом:
враг — врач — грач — граб — краб — крап — круп — круг — друг;

Как лиса добралась до норы:
лиса — липа — лапа — папа — пара — пора — нора;

Что поможет ребёнку решать задачи

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:

• Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.   

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4· равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.

Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе. 

Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

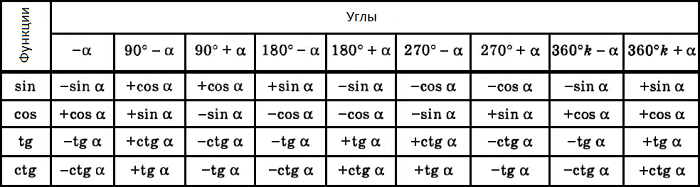
Формулы приведения задаются в виде таблицы:

Примеры умножения дробей с переменными

При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.

Пример 8

Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.

Решение

Необходимо выполнить умножение. Получаем, что

x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)

Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида

3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)

Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).

Примеры сложения и вычитания дробей с переменными

Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это  незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 6

Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.

Решение

1. Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2.  После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
2. Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:​​​​​​lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
   Сложение было выполнено. Видно, что можно произвести сокращение дроби.  Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, чтоlg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x
3.  Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.

Рассмотрим двоякий способ решения.

Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида

x-1x-1=x-1(x-1)·x+1=1x+1

Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.

В таком случае необходимо избавляться от иррациональности в знаменателе.

Получим:

1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1

Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда

x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1

Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.

В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей  с добавлением дополниетльных множителей к числителям.

Пример 7

Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x

Решение

1.  Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
2. Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться  произведение вида x5·ln2x+1·2x-4. Отсюда x4является дополнительным множителем к первой дроби, а ln(x+1)ко второй. После чего производим вычитание и получаем, что:x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)
3.  Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2.  Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.

После чего получаем, что

1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2

Ответ:

1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

   6x −5x = 10

2. Приведем подобные и завершим решение.

   x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

   −4x = 12 | :(−4)
   x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Шаблон сочинения ЕГЭ

1. Вступление — 2-3 предложения подводящие к проблеме. Можно не использовать вступление, а сразу перейти к риторическому вопросу и перейти к формулировке проблемы.

Клише для вступления:

• Думаю, эта тема интересует многих….
• Не ошибусь, если скажу, что данная тема актуальна для большинства…
• Об этом написано много произведений и снято тысячи кинолент…
• Всем известен факт…

2. Формулировка проблемы (К1) — размышление автора над поставленной проблемой.

Клише для формулировки проблемы:

Автор текста (ФИО) размышляет над проблемой (чего?)… Автор текста (ФИО) предлагает своим читателям задуматься над проблемой (чего)… В центре внимания автора текста (ФИО) проблема (чего?)… Проблемный вопрос. Этой проблеме посвящен текст автора (ФИО)

Именно эта проблема привлекла внимание автора текста (ФИО)

3. Комментарий к проблеме (К2) — пять шаблонов: 2 примера-иллюстрации из прочитанного текста, важны для понимания проблемы исходного текста, 2 пояснения и смысловая связь между ними..(вывод, противопоставление, сравнение). ПОМНИ! Комментарий — это не пересказ. Если какого-то элемента из шаблона нет, то баллы снижаются.

Клише для комментариев:

Примеры – иллюстрации В качестве примера автор рассматривает… Проблема раскрывается автором на примере… Автор обращает внимание читателя на … Пояснение к примерам Этот пример показывает, что… Этот пример убедительно доказывает, что… Эти события(факты, примеры) помогают понять… Связь между примерами Размышляя над проблемой, автор противопоставляет…. Для сравнения автор обращается к … Оба примера, дополняя друг друга, дают ясно понять…

4. Авторская позиция (К3) — позиция автора исходного текста раскрывается в конце, где автор дает ответ на проблемный вопрос.

Клише для отображения авторской позиции:

• Автору удалось убедить читателя в том, что…
• В произведении доказана мысль о…
• Позиция автора такова…
• «Цитата из текста, где явно звучит вывод автора»

5. Ваше отношение к позиции автора(К4)— своё отношение к позиции автора текста по проблеме (согласившись или не согласившись с автором) + обоснование.

Клише для выражения собственного мнения:

Твое отношение к позиции автора	Я согласен с мнением автора. Не могу полностью разделить мнение автора… Безусловно, автор прав. Моя точка зрения совпадает с позицией автора… Трудно не согласиться с автором. Я полностью разделяю позицию автора.
Обоснование собственной позиции	Нельзя не вспомнить героя известного фильма/ романа… Сама история человечества не раз доказывала справедливость этого… Известный ученый/ писатель/ деятель/… об этом говорил так…

6. Вывод — обобщение твоего рассуждения. Подводятся итоги в 2-3 предложениях.

Клише для вывода:

После прочтения этого произведения становится понятно… После знакомства с героями произведения понимаешь… Прочитав произведение, осознаешь… Автор стремился показать..

Автор хочет, чтобы читатель понял… Автор текста считает проблему важной…

Смотри также:

• План
• Критерии оценивания от ФИПИ
• Речевые клише
• Цитаты
• Требования к оформлению
• 10 важных советов при написании сочинения

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Примеры видов

Белые медведи и гризли

Часто единственным барьером для размножения является географическое или основанное на физическом местонахождении животных. Если это изменится, животные могут скрещиваться и могут сливаться в один вид. В настоящее время это наблюдается в дикой природе у белых медведей и медведей гризли. По мере изменения климата белые медведи вынуждены двигаться дальше на юг и должны начать использовать различные источники пищи. Изменение климата также позволяет медведям гризли идти дальше на север, встречая на пути белых медведей. Ранее разделенные популяции теперь имеют возможность размножаться, и иногда они успешны. Гибриды были замечены в дикой природе, но еще не известно, будут ли они гибридами успешными.

Существует множество различных ситуаций и примеров репродуктивных барьеров, но если этот барьер удастся устранить, вполне вероятно, что два родственных вида смогут скрещиваться. Несвязанные виды редко имеют возможность размножаться, потому что они стали слишком отличаться друг от друга. Например, летучая мышь и черепаха имеют совершенно разную генетическую структуру. Гены, которые контролируют рост черепахи, не будут функционировать у летучих мышей, и наоборот. На самом деле, они даже не имеют одинакового количества хромосом, что является условием для полового размножения организмов, чтобы быть успешным.

Собаки и волки

Тем не менее, другие животные, такие как собаки и волки, технически все те же виды. Хотя они имеют одинаковое количество хромосом и могут технически размножаться, домашняя собака прошла долгий путь от своего дикого аналога. Собаки не только стали более приятными и мягкими, но и настроены на социальные сигналы человека. Волки действуют в совершенно другой социальной структуре. Таким образом, эти два вряд ли будут размножаться в реальном мире. Однако, поскольку они могут создавать плодовитое потомство, ученые считают их одним и тем же видом.

Собаки и волки являются хорошим примером радиации видов или постепенного изменения Население это широко распространено. Подумайте о чихуахуа. Если бы Линней классифицировал это животное, он бы не отнес его к той же категории, что и волк. Тем не менее, чихуахуа может размножаться с немного большей собакой, которая может размножаться с большой собакой, которая может легко размножаться с волком. Таким образом, чихуахуа и волк имеют одну и ту же генетическую основу, выраженную по-разному.

• Гибридный – Организм, созданный скрещиванием двух разных видов.
• Репродуктивные барьеры – препятствия, мешающие двум животным производить плодовитое потомство.
• Биноминальная номенклатура – Система именования отдельных видов двумя латинскими названиями, первое относится к их роду, второе – к их виду.
• Таксономическая иерархия – Система, в которую помещаются все организмы для классификации.